Программирование в Gambas. Урок 2
Методические материалыАвтор: Владимир Черный
Второй урок по Gambas от Олега Чебан из из г. Киселевск Кемеровской области. Первый урок тут.
Урок 2. Построение графиков функций в Gambas.
Тип урока: Лабораторная работа. Полное учебное занятие.
Цель урока:
- Приобрести первичные навыки по использованию графических примитивов в Gambas.
- Познакомиться со способом инициализации свойств объектов на программном уровне.
- Закрепить знания по использованию оператора выбора (Select Case).
- Научиться создавать функции с одним выходным параметром.
- Осуществить межпредметную связь с курсом математики.
Задача. Написать программу построения графиков функциональных зависимостей от одной переменной.
Постановка задачи.
- Для построения графиков используем область рисования Drawingarea. Для ввода функции текстовое поле TextBox. Построение осуществим по кнопке Button. Внешний вид программы см. Рис. 1. Масштаб: 1 к 30 пикселей.
Рис. 1. Внешний вид программы.
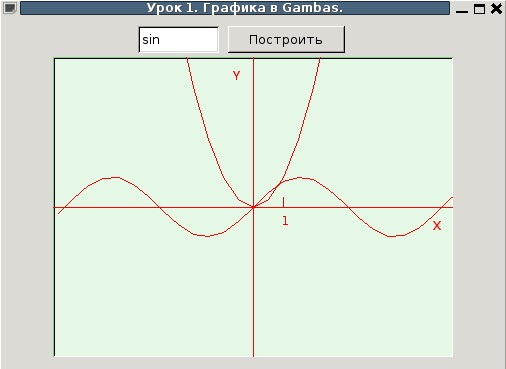
- Всего построим 3 функции: Sin(x), Cos(x) и квадратичная X^2, см. табл.1
Табл. 1. Математические функции Gambas.
| Функция | Описание |
| Abs(x) | Модуль числа X |
| Log(x) | Натуральный логарифм от X |
| Log10(x) | Десятичный логарифм от X |
| Sin(x) | Синус от X, угол в радианах |
| Cos(x) | Косинус от X, угол в радианах |
| Tan(x) | Тангенс от X |
| ASin(x), Acos(x), ATan(x) | Арксинус, арккосинус, арктангенс |
| Sqr(x) | Корень квадратный из X |
| Randomize | Регенерация датчика псевдослучайных чисел |
| RND | Псевдослучайное число от 0 до 1, тип Float (действительный) |
| RND(3) | Псевдослучайное число от 0 до 3 |
- Требования к задаче:
- инициализацию свойств объектов осуществить в программной части;
- построение кривой осуществить с помощью «ломанной» линии Draw.Line;
- масштаб определить как 1:30.
Ход работы:
- Предварительные сведения.
К объектам системы Gambas можно применить предопределенные свойства и методы. Сначала пишем имя объекта и через точку указываем свойство (синий кружок), или метод (зеленый). Например, объекту текстовое поле TextBox: зададим свойство text — TextBox.text = «33.55 руб.», или метод TextBox.clear — очистить содержимое текстового поля.
- Инициализацию свойств осуществим в конструктуре _new:
| ‘Процедура _new — это конструктор. Используя его, мы можем устанавливать разные заголовки, ‘этикетки и содержание текстовых вводов каждый раз, когда используется диалог. ‘Более того, эти свойства устанавливаются в момент создания. PUBLIC SUB _new() ME.Caption = «Урок 1. Графика в Gambas.» ‘иницализируем/задаем заголовок формы ‘ или так Form.Text = «Урок 1. Графика в Gambas» FMain.Center ‘Форма по центру экрана FMain.Width = 500 ‘Ширина формы FMain.Height = 400 ‘Высота формы DrawingArea1.X = 50 ‘Координаты левого верхнего угла объекта DrawingArea DrawingArea1.Y = 40 DrawingArea1.Width = 400 ‘Ширина объекта DrawingArea DrawingArea1.Height = 300 ‘Высота DrawingArea DrawingArea1.Background = 15071461 ‘Цвет фона DrawingArea — светлозеленый DrawingArea1.ForeColor = 16711937 ‘Оси — цвет красный Button1.text = «Построить» TextBox1.text = «sin» END |
- Вычисляемая функция принимает два параметра: strFunc — функция введенная пользователем (например sin) и fltX — значение Xi. Возвращает результат — Yi
| ‘Функция вычисления аргумента SUB trigonometria(strFunc AS String, fltX AS Float) AS Float SELECT CASE strFunc CASE «sin» RETURN Sin(fltX) CASE «cos» RETURN Cos(fltX) CASE «x^2″ RETURN fltX ^ 2 CASE ELSE RETURN 255 END SELECT END |
- Строим график.
Объект рисунок «DrawingArea» находится во вкладке Container:
Размеры холста DrawingArea мы определи в 400 на 300 точек, значения инициализировали в конструкторе _New, как Fmain.Width=400 (ширина) и Fmain.Height=300 (высота).
Предполагается построить тригонометрическую функцию Sin(x) и Cos(x) на отрезке от -2*Pi (~ -6.28) до +2*Pi (~ +6.28) с шагом табулирования 0.5. Поэтому числовой отрезок по X выглядит так:
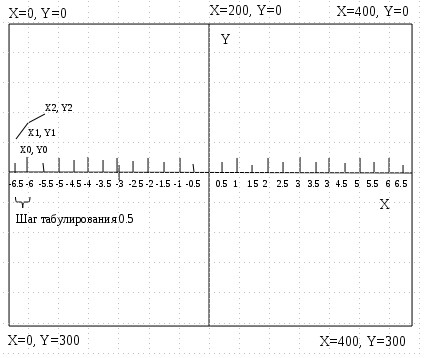
Кривую построим из отрезков [X0, Y0]-[X1, Y1] и т.д.. Всего получается 27 отрезков, количество итераций в цикле 26-ть, соответственно.
- Процедура «Клик по кнопке».
| PUBLIC SUB Button1_Click() DIM i AS Byte DIM m AS Byte ‘Масштаб DIM x AS Float[128] DIM y AS Float[128] ‘К объекту Draw (Рисунок) применить метод Начать DRAW.BEGIN(DrawingArea1) Draw.Line(200, 0, 200, 300) Draw.Text(«X», 380, 160) ‘подписать оси Draw.Line(0, 150, 400, 150) Draw.Text(«Y», 180, 10) Draw.Line(230, 140, 230, 150) ‘масштабная единица Draw.Text(«1″, 228, 155) m = 30 ‘масштаб 30 точек x[0] = -6.5 ‘нач. значение X y[0] = trigonometria(TextBox1.text, x[0]) ‘ передача параметров функции x[1] = x[0] + 0.5 ‘шаг табулирования 0.5 ‘Если нет в списке функции, то вывести предупреждение и выполнить рекурсию IF y[0] = 255 THEN Message.error(«Нет такой функции!») _new ‘рекурсия — перезапуск формы END IF FOR i = 1 TO 26 STEP 1 y[i] = trigonometria(TextBox1.text, x[i]) Draw.Line(200 + x[i — 1] * m, 150 — y[i — 1] * m, 200 + x[i] * m, 150 — y[i] * m) x[i + 1] = x[i] + 0.5 NEXT ‘Применить метод окончить DRAW.END() END |
Домашнее задание.
Изменить программу таким образом, чтобы выбор вычисляемых функций выбирался пользователем с помощью раскрывающегося списка ComboBox.
1. Вставка функций осуществляется в Панели свойств → свойство List, см. Рис. 2.
Рис. 2.a. Свойство List
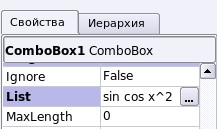
Рис. 2.b. Значения List
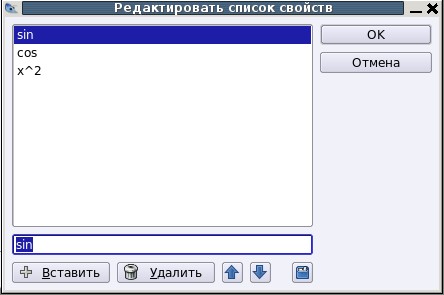
2. Значения List можно получить по команде: ListBox1.List[0] — первое значение (в нашем случае «sin»), ListBox1.List[1] — второе значение («cos») и т.д..
Copyleft © Oleg Tcheban
ГОУ СПО Киселевский педагогический колледж


Апрель 27, 2011, 8:07 дп
По ходу освоения системы Gambas, нами были обнаружены следующие преимущества:
1. Синтаксис управляющих конструкций практически не отличается от «классического» BASIC, т.е. вопрос переучивания языковых конструкций отпадает.
2. Интерфейс системы схож с VisualBasic 6.0, который фактически стал базовым для учителей информатики практикующих на Бейсике.
3. Возможность компиляции кода (Проект -> Собрать -> Запускаемые).
4. Возможность сборки инсталяционного пакета для различных Linux-систем (Проект -> Собрать -> Инсталяционный пакет).
5. Интерфейс системы не загружен, как например в Lazarus.
6. Считаем, что визуальное программирование для графической части системы, поможет катализировать интерес учащихся к практическому программированию, которое в свою очередь научит детей систематизировать вал информации, выработает необходимые навыки для «хорошей» постановки задач в различных сферах человеческой деятельности, разовьет алгоритмическое мышление, расширит знания в пограничных естественно-научных дисциплинах.. В общем, подготовит молодых людей к серьезному самообразованию в дальнейшей профессиональной деятельности, будь-то врач, проектировщик, оператор станка с ЧПУ..
—
Недостатки:
1. Небольшое количество Gambas-примеров на русском языке. Временно