СПО в российских школах

Метод Монте-Карло на уроке информатики

Тема моделирования реальных процессов наиболее сложная в курсе информатики, поскольку требует от учеников осознанной интеграции знаний из разных областей знаний.
Сегодня мы предлагаем вашему вниманию разработку урока к разделу «Вероятностные модели, Метод Монте-Карло» учебника Угриновича. Разработку, с использованием Gambas, подготовила учитель информатики МБОУ «Гимназия №85» г. Барнаула (Алтайский край) Чупина Татьяна Ивановна. К тексту урока прилагается презентация (ее желательно скачать до начала чтения статьи) и проект для Gambas.

Построение вероятностных моделей. Метод Монте-Карло

Конспект урока
Автор: Чупина Татьяна Ивановна, учитель информатики МБОУ «Гимназия №85» г. Барнаула
Тема урока: Построение вероятностных моделей. Метод Монте-Карло
Предмет: информатика и ИКТ
Класс: 11
Учебник: Угринович Н. Д. 11 класс (профильный уровень)
Тип урока: лабораторная работа (пара — 2 урока)
Цели урока:
Обучающая:
получить представление о методе Монте-Карло, как способе поиска площади фигур, закрепить знания по использованию графических операторов, учить решать практические задачи компьютерными средствами, осуществить межпредметную связь с математикой.
Воспитательная: воспитывать трудолюбие
Развивающая: развивать способность к анализу и синтезу, к аналогии.
Характеристика класса: профильный физико-математический
Средства, обеспечивающий учебный процесс на уроке: компьютерный класс с предустановленной ОС Linux и средой программирования Gambas, проектор.

Деятельность учащихся	Деятельность учителя
Организационный момент
Учащиеся располагаются за рабочими местами, оборудованными компьютерами	Учитель приветствует учащихся
Опрос учащихся по заданному на дом материалу
Числовые – Integer, Float, Long, Byte, Short, символьные – String, логические –Boolean. For i= to k Step s Next Do While условие Loop RND() – генератор случайных чисел VAL() – преобразует число в строку и наоборот Растровая (изображение состоит из пикселей) и векторная (изображение состоит из примитивов)	Слайд 1 Фронтальный опрос с целью актуализации знаний
Проблемная ситуация
Площадь прямоугольника – ab Площадь круга – Pi*r2 r2(4-Pi) Для нахождения площади произвольной фигуры «наложить сетку», найти количество целых квадратов и прибавить количество частей деленное на два. Единицы измерения зависят от размера одной клетки. Растровое изображение состоит из пикселей. Необходимо посчитать количество пикселей внутри фигуры	Слайд 2, Слайд 3 Фронтальный опрос с целью постановки практической задачи урока.
Изучение нового учебного материала
Учащиеся конспектируют материал, отвечают на вопросы. Записи в тетради: Тема (слайд 4) Понятие вероятностной модели (слайд 5) Описательная модель включая рисунок Формальная модель	Слайды 4-10, Формулируется тема, оформляется конспект урока
Лабораторная работа
N, R Float TextBox DrawingArea Заливать цветом фона	Обсуждение элементов графического интерфейса в форме беседы 1. Какие переменные нужно ввести? 2. Какого типа переменные? 3. Какие объекты будем использовать для ввода этих переменных? 4. Какой объект будем использовать для отображения рисунка? 5. Каким образом можно реализовать действие кнопки «Очистить»?
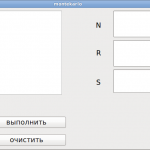
Учащиеся создают окно программы.	Учитель на своём компьютере параллельно с учащими воспроизводит все этапы создания графического интерфейса программы. (Слайд 11)
Щелчок по кнопке «выполнить»	Какое действие и над каким объектом необходимо выполнить для произведения расчетов?
1. DIM 2. DIM r, x, y, m AS Float ‘r — радиус, x,y — кооодинаты точек-снежинок-зёрен, m — количество точек попавших в окружность, DIM i, n AS Integer ‘n — количество выстрелов-бросаний всего, i-счетчик 3. Текстовая 4. Нет 5. n = Val(TextBox1.Text) ‘преобразуем текстовое значение в числовое, r = Val(TextBox2.Text)	(В ходе беседы учитель последовательно с учениками добавляет строки в программу, соответствующие ответам учащихся.) 1. С какого служебного слова начинается блок описания переменных? 2. Какие переменные и какого типа необходимо использовать? 3. Какого типа будет информация вводимая в TextBox? 4. Возможно ли выполнять арифметические действия над данными такого типа? 5. Как перевести строку в число?
Цикл – FOR FOR i = 1 TO n x = Int(Rnd(2 * r) — r) y = Int(Rnd(2 * r) — r) Draw.Forecolor = &ff0000& ‘цвет снежинки Draw.Circle(x + 100, y + 100, 2) ‘рисование зерен-выстрелов-снежинок IF (x ^ 2 + y ^ 2) <= r ^ 2 THEN m = m + 1 NEXT	Принцип работы: генерируем х и у, рисуем точку, генерируем, рисуем … С помощью какого оператора можно организовать многократное поврорение?
Объект TextBox3, свойство Text TextBox3.Text = 4 * (r ^ 2) * m / n	Какой объект и какое свойство изменится при выводе S?
PUBLIC SUB Button2_Click() Draw.Begin(DrawingArea1) Draw.FillColor = &ffffff& ‘белый цвет заливки Draw.FillStyle = 1 ‘сплошная заливка Draw.ForeColor = &ffffff& ‘белый цвет границы Draw.Rect(0, 0, 400, 400) ‘очистка DrawingArea1 путём рисования белого прямоугольника Draw.End END	Запрограммируйте кнопку «очистить» самостоятельно.
Учащиеся запускают и проверяют работоспособность, исправляют ошибки.	Учитель демонстрирует конечный программный код. Слайд 12
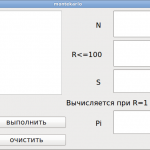
Учащиеся изучают материал параграфа, вывод формулы. Изменяют интерфейс программы в соответствии с заданием. TextBox4.Text = 4 * m / n	Работа с учебником. Задание: Найти приблизительное значение числа Pi.
Подведение итогов
1. Чем больше N тем точнее вычисление 2. Пиксели 3. Да, если даны уравнения прямых, задающих этот треугольник 4. При N-максимальном, R=1	(Слайд 14 Фронтальный опрос) 1. Установите зависимость между количеством точек (N) и точностью вычисления площади фигуры? 2. Назовите единицу измерения площади фигуры в программе? 3. Можно ли с помощью этого метода определить площадь треугольника? 4. При каких параметрах значение числа Пи находится с максимальной точностью?
Задание на дом
Учащиеся записывают задачу в тетрадь	(Слайд 15) В тетради изобразите в координатной плоскости фигуру заданную координатами её вершин. Составьте условие принадлежности точки (x;y) этой фигуре: (0;1),(1;0),(-1;0)

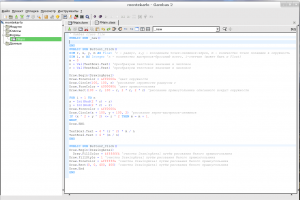
Код программы в редакторе.

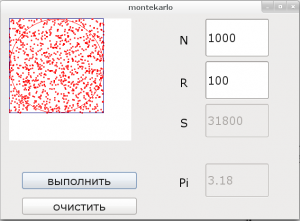
Выполнение программы.

Презентация к уроку
Проект Gambas