СПО в российских школах

BASIC-256. Глава 14

Продолжаем публиковать перевод книги Джеймса Рено. Эту главу перевел Владимир Черный.
Оглавление:

• Глава 1: Знакомство с BASIC-256 – cкажи «Привет»
• Глава 2: Рисуем основные фигуры
• Глава 3: Звуки и музыка
• Глава 4: Мыслить как программист
• Глава 5: Программа задает вам вопросы
• Глава 6: Сравнения, сравнения, сравнения
• Глава 7: Циклы и счетчики — повторяем снова и снова
• Глава 8: Графика на заказ — создание фигур своими руками
• Глава 9: Подпрограммы — повторное использование кода
• Глава 10: Управляем мышкой, перемещаем объекты
• Глава 11: Использование клавиатуры для управления программой
• Глава 12: Картинки, музыка и спрайты
• Глава 13 Массивы — коллекции данных

Где взять BASIC-256

Глава 14. Математика — развлечемся с числами

В этой главе мы рассмотрим некоторые дополнительные математические операторы и функции. Глава разбита на 4 части: 1) новые операторы 2) новые целые функции 3) новые функции для работы с числами с плавающей точкой (действительные числа), и 4) тригонометрические функции.

Новые операторы

В дополнение к базовым математическим операциям, которые мы использовали с первой главы книги, есть еще три оператора в BASIC-256. Операции, аналогичные этим есть в большинстве языков программирования. Это операция деления по модулю, целочисленного деления и возведения в степень.

Деление по модулю

Операция деления по модулю возвращает остаток от деления нацело. Когда вы делите два целых числа «уголком», остаток, полученный в результате и есть модуль.


1 # c12_mod.kbs
2 input "Введите целое число ", n
3 if n % 2 = 0 then print "делится на 2"
4 if n % 3 = 0 then print "делится на 3"
5 if n % 5 = 0 then print "делится на 5"
6 if n % 7 = 0 then print "делится на 7"
7 end


Программа 78 Деление по модулю

Введите целое число 10
делится на 2
делится на 5

Пример вывода программы 78 Деление по модулю

выражение1 % выражение2 Оператор деления по модулю (%) возвращает остаток от деления числа выражение1 на число выражение2 Если одно или оба выражения не целые, то сначала они округляются до целого отбрасыванием дробной части (как это делает функция int() ) до того, как операция будет произведена.

Вы может и не задумывались, но операция деления по модулю используется программистами довольно часто. Основные два применения это 1) проверить делится ли одно число на другое (программа 78) и 2) получить числа из ограниченного диапазона (программа 79)


 1 # moveballmod.kbs
 2 # Переписанная программа moveball.kbs с использованием оператора
 3 # деления по модулю для ограничения движения мяча экраном
 4
 5 print "клавиша i - вверх, j - влево, k - вправо, m - вниз, q - закончить"
 6
 7 fastgraphics
 8 clg
 9 ballradius = 20
10
11 # позиция мяча
12 # начинаем с центра экрана
13 x = graphwidth /2
14 y = graphheight / 2
15
16 # рисуем мяч в начальном положении на экране
17 gosub drawball
18
19 # цикл ожидания ввода пользователем нажатий на клавиши
20 while true
21    k = key
22    if k = asc("I") then
23    # y может стать отрицательным, + graphheight делает это число положительным
24        y = (y - ballradius + graphheight) % graphheight
25        gosub drawball
26    end if
27    if k = asc("J") then
28        x = (x - ballradius + graphwidth) % graphwidth
29        gosub drawball
30    end if
31    if k = asc("K") then
32        x = (x + ballradius) % graphwidth
33        gosub drawball
34    end if
35    if k = asc("M") then
36        y = (y + ballradius) % graphheight
37        gosub drawball
38    end if
39    if k = asc("Q") then end
40 end while
41
42 drawball:
43 color white
44 rect 0, 0, graphwidth, graphheight
45 color red
46 circle x, y, ballradius
47 refresh
48 return

Программа 79 Двигаем мяч с использованием деления по модулю.

Целочисленное деление

Операция целочисленного деления (\) производит обычное деление, но работает только с целыми числами и возвращает целое число. Например 13 разделить на 4 будет 3 и в остатке 1. Результатом операции целочисленного деления будет 3.

1 # c12_integerdivision.kbs
2 input "Делимое ", dividend
3 input "Делитель ", divisor
4 print dividend + " / " + divisor + " = частное ";
5 print dividend \ divisor;
6 print " и остаток (r) ";
7 print dividend % divisor;


Программа 80 Проверь как ты делишь уголком

Делимое 43
Делитель 6
43 / 6 = частное 7 и остаток (r) 1

Пример вывода программы 80 Проверь как ты делишь уголком

выражение1 \ выражение2 Целочисленное деление (\) делит выражение1 на выражение2 и в качестве результата возвращает целое число, которое показывает во сколько раз выражение1 больше выражение2 (частное от деления) Если одно или оба числа не целые, они округляются до целого, отбрасыванием десятичной части (как это делает int()) до того, как операция будет произведена.

Возведение в степень

Оператор возведения в степень возвращает степень первого числа относительно второго.

1 # c12_power.kbs
2 for t = 0 to 16
3 print "2 ^ " + t + " = ";
4 print 2 ^ t
5 next t

Программа 81 Степени числа 2

2 ^ 0 = 1
2 ^ 1 = 2
2 ^ 2 = 4
2 ^ 3 = 8
2 ^ 4 = 16
2 ^ 5 = 32
2 ^ 6 = 64
2 ^ 7 = 128
2 ^ 8 = 256
2 ^ 9 = 512
2 ^ 10 = 1024
2 ^ 11 = 2048
2 ^ 12 = 4096
2 ^ 13 = 8192
2 ^ 14 = 16384
2 ^ 15 = 32768
2 ^ 16 = 65536

Примерный вывод программы 81 Степени числа 2

выражение1 ^ выражение2 Оператор степень (^) возводит выражение1 в степень заданную числом выражение2. Математическая запись степени a = bc в BASIC-256 записывается как a = b^c

Новые целочисленные функции

Три новые функции этой главы связаны с преобразованием строк и чисел с плавающей точкой (действительных чисел) в целые числа. Все три эти функции по разному обрабатывают десятичную часть числа.

Функция int() просто отбрасывает десятичную часть числа, что равносильно вычитанию дробной части от (положительного) числа или прибавления десятичной части к отрицательному числу. Это может привести к проблемам, если мы пытаемся округлить числа меньшие нуля (0).

Функции ceil() и floor() по своему решают проблему int(). Функция ceil() дополняет дробное число до ближайшего целого, большего, чем исходное число, в то время как floor() всегда уменьшает число до ближайшего целого, меньшего данного числа.

Всех нас учили округлять, прибавляя 0.5 и отбрасывать дробную часть. Если мы используем int(), то она работает с положительными числами и не работает с отрицательными. В BASIC-256 для округления («как привычно») следует использовать формулу типа a=floor(b+0.5) .

Функция Описание int(выражение) Преобразует выражение (строку, целое или десятичную дробь) в целое число. При этом дробная часть просто отбрасывается. Если строка не содержит числа возвращается нуль. ceil(выражение) Преобразует выражение в ближайшее большее целое floor(выражение) Преобразует выражение в ближайшее меньшее целое. Для округления следует использовать формулу a=floor(b+0.5)


1 # c12_intceilfloor.kbs
2 for t = 1 to 10
3     n = rand * 100 - 50
4     print n;
5     print " int=" + int(n);
6     print " ceil=" + ceil(n);
7     print " floor=" + floor(n)
8 next t

Программа 82 Различие между int, ceil и floor

-34,342984 int=-34 ceil=-34 floor=-35
23,295121 int=23 ceil=24 floor=23
-25,956241 int=-25 ceil=-25 floor=-26
10,697896 int=10 ceil=11 floor=10
-16,144697 int=-16 ceil=-16 floor=-17
44,576658 int=44 ceil=45 floor=44
35,383576 int=35 ceil=36 floor=35
4,651446 int=4 ceil=5 floor=4
-39,022827 int=-39 ceil=-39 floor=-40
47,965051 int=47 ceil=48 floor=47

Примерный вывод программы 82 Различие между int, ceil и floor

Новые функции для дробных чисел

Математические функции, в которые погрузила нас эта глава могут пригодиться при написании некоторых специальных программ. В подавляющем большинстве программ они не нужны.

Функция Описание float(выражение) Преобразует выражение (строку, целое или десятичную дробь) в дробное число. Обычно используется для преобразования строк в числа. Если строка не содержит числа возвращается нуль. abs(выражение) Возвращает беззнаковое значение выражения (абсолютное значение) log(выражение) Возвращает натуральный логарифм числа (логарифм по основанию e) log10(выражение) Возвращает десятичный логарифм числа (логарифм по основанию 10)

Тригонометрические функции (для знакомых с ними)

Тригонометрия — наука об измерении углов и сторон (и их соотношений) в треугольнике. BASIC-256 поддерживает основные тригонометрические функции. Углы измеряются в радианах (0-2π). Если вы хотите использовать градусы (0-360) в своей программе, то необходимо значения в градусах предварительно преобразовать в радианы, а потом использовать в тригонометрических функциях.

Функция Описание cos(выражение) Возвращает значение косинуса угла sin(выражение) Возвращает значение синуса угла tan(выражение) Возвращает значение тангенса угла degrees(выражение) Преобразует число из радиан (0-2π) в градусы (00 3600) radians(выражение) Преобразует число градусов (00 3600) в радианы (0-2π) acos(выражение) Функция, обратная косинусу (арккосинус) asin(выражение) Функция, обратная синусу (арксинус) atan(выражение) Функция, обратная тангенсу (арктангенс)

Первые три функции имеют прямое отношение к сторонам прямоугольного треугольника. Рисунок 20 демонстрирует прямоугольный треугольник, его стороны и углы.

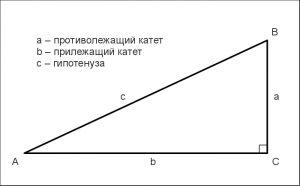
Рисунок 20 Прямоугольный треугольник.

Косинус

Косинус угла равен отношению прилежащего катета к гипотенузе:
.
Косинус повторяет свои значения в диапазоне от -1 до 1 на каждом интервале длиной 2π радиан. Рисунок 21 показывает волновой график косинуса в диапазоне от 0 до 2π.

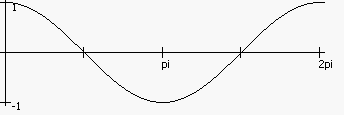
Рисунок 21 Функция cos()

Синус

Синус равен отношению прилежащего катета к гипотенузе:
.
Синус также, как и косинус повторяет свои значения из диапазона от -1 до 1 на каждом интервале длиной 2π

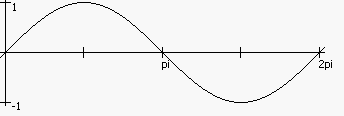
Рисунок 22 Функция sin()

Тангенс

Тангенс равен отношению противолежащего катета к прилежащему:
.
Тангенс повторяет свои значения лежащие в диапазоне от -∞ до ∞ на каждом отрезке в π радиан. Такой диапазон тангенса объясняется тем, что когда угол треугольника становится очень маленьким, противолежащий катет становится очень маленьким.

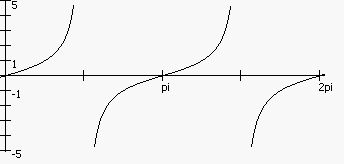
Рис. 23 Функция tan()

Функция degrees

Функция degrees() преобразует значения угла из радиан в градусы по формуле: градусы = (радианы/2π)*360.

Функция radians

Функция radians() преобразует значения угла из градусов в радианы по формуле радианы = (градусы/360)*2π Запомните, все тригонометрические функции BASIC-256 используют в качестве аргумента радианы, а не градусы.

Арккосинус

Арккосинус (acos()) — функция обратная косинусу. Ее значением является величина угла, косинус которого равен заданному числу.

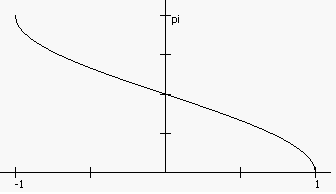
Рисунок 24 Функция acos()

Арксинус

Арксинус (asin()) – функция, обратная синусу. Ее значением является величина, синус которого равен заданному числу.

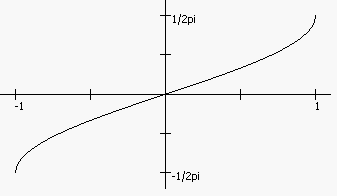
Рисунок 25 Функция asin()

Арктангенс

Арктангенс (atan()) – функция, обратная тангенсу. Ее значением является угол, тангенс которого равен заданному числу.

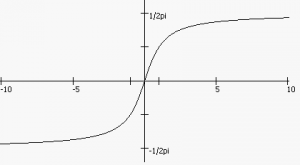
Рисунок 26 Функция atan()

Большая программа этой главы воспроизводит процесс деления целых чисел уголком. Программа использует логарифм, чтобы вычислить количество знаков в числах, деление по модулю и целочисленное деление для определения цифр, и в целом очень сложная программа. Не расстраивайтесь и не опускайте руки, если сразу не поймете в полностью, как она работает.


 1 # longdivision.kbs
 2 # Показывает графически процесс деления уголком
 3 # двух положительных целых чисел.
 4
 5 input "Делимое? ", b
 6 input "Делитель? ", a
 7
 8 originx = 100
 9 originy = 20
10 height = 12
11 width = 9
12 margin = 2
13
14 b = int(abs(b))
15 a = int(abs(a))
16
17 color white
18 rect 0,0,graphwidth, graphheight
19 color black
20
21 # Отображение задания на деление
22 row = 0
23 col = -1
24 number = a
25 underline = false
26 gosub drawrightnumber
27 row = 0
28 col = 0
29 number = b
30 gosub drawleftnumber
31 line originx - margin, originy, originx + (width * 11), originy
32 line originx - margin, originy, originx - margin, originy + height
33
34 # Сколько цифр в делимом?
35 lb = ceil(log10(abs(b)))
36
37 r = 0
38 bottomrow = 0    ## номер последнего ряда вычислений
39
40 # Цикл по всем цифрам слева направо
41 for tb = lb-1 to 0 step -1
42    # получаем следующюю цифру текущего остатка и убираем ее из делимого
43    r = r * 10
44    r = r + (b \ (10 ^ tb))
45    b = b % (10 ^ tb)
46    # отображаем текущий остаток
47    row = bottomrow
48    bottomrow = bottomrow + 1
49    col = lb - tb - 1
50    number = r
51    underline = false
52    gosub drawrightnumber
53    # вычисляем следующую цифру ответа и отображаем ее
54    digit = r \ a
55    row = -1
56    col = lb - tb - 1
57    gosub drawdigit
58    # вычисляем количество которое надо удалить из текущего остатка и отображаем
59    number = digit * a
60    r = r - number
61    col = lb - tb - 1
62    row = bottomrow
63    bottomrow = bottomrow + 1
64    underline = true
65    gosub drawrightnumber
66 next tb
67 #
68 # печатаем остаток в нижнем ряду
69 row = bottomrow
70 col = lb - 1
71 number = r
72 underline = false
73 gosub drawrightnumber
74 end
75
76 drawdigit:
77 # вычисляем строку и столбец для отображения
78 text col * width + originx, row * height + originy, digit
79 if underline then
80    line col * width + originx - margin, (row + 1) * height + originy, (col + 1) * width + originx - margin, (row + 1) * height + originy
81 end if
82 return
83
84 drawleftnumber:
85 # передаем начальный ряд и колонку, а также число для левой колонки
86 if number < 10 then
87    digit = number
88    gosub drawdigit
89 else
90    lnumber = ceil(log10(abs(number)))
91    for tnumber = lnumber-1 to 0 step -1
92        digit = (number \ (10 ^ tnumber)) % 10
93        gosub drawdigit
94        col = col + 1
95    next tnumber
96 endif
97 return
98
99 drawrightnumber:
100 # передаем начальный ряд, колонку и число для отображения в правой колонке
101 if number < 10 then
102    digit = number
103    gosub drawdigit
104 else
105    lnumber = ceil(log10(abs(number)))
106    for tnumber = 0 to lnumber - 1
107        digit = (number \ (10 ^ tnumber)) % 10
108        gosub drawdigit
109        col = col - 1
110    next tnumber
111 endif
112 return

Программа 83 Большая программа Деление уголком

Делимое? 123456
Делитель? 78


Пример вывода программы 83 Большая программа Деление уголком

============================

Где скачать BASIC-256:

Для дистрибутивов ALT Linux

• ветка 4.0 basic256-0.9.6-alt5.M40.1.i586.rpm
• ветка 4.1 basic256-0.9.6-alt5.M41.1.i586.rpm
• ветка p5 basic256-0.9.6-alt5.M50P.1.i586.rpm
• ветка 5.1 basic256-0.9.6-alt5.M51.1.i586.rpm

Windows версия
http://basic256.org (http://www.sourceforge.net/projects/kidbasic)

Как установить BASIC-256 в Linux

Для Альт Линукс: настроить репозиторий и обновить/установить пакет через synaptic или apt
Для rpm-based дистрибутивов: rpm -Uvh <имя_пакета>.rpm