СПО в российских школах

Команда ALT Linux рассказывает о внедрении свободного программного обеспечения в школах России
Апрель 28, 2011

Программирование в Gambas. Урок 3

Методические материалы
Автор: Владимир Черный

Еще один урок по Gambas от Олега Чебан из из г. Киселевск Кемеровской области.
Первый урок
Второй урок

Урок 3. Артиллерийская задача.
Движение тела, брошенного под углом к горизонту.

Тип урока: Лабораторная работа.

Цель урока: Приобрести первичный опыт компьютерного исследования физических процессов.

Оборудование: Проектор.

Ход работы.

Задача. Рассмотрим движение тела (снаряда) брошенное (пущенное) под углом.
Под телом понимаем материальную точку. Для упрощения модели сопротивлением воздуха и массой тела пренебрегаем.

Математическая модель.

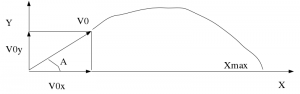
Уравнения движение точки:
X=V0x*t, где V0x=V0*Cos(A)
Y=V0y*t-(g*t^2)/2, где V0y=V0*Sin(A)

Для нахождения уравнения траектории движения из системы уравнений исключаем время:
t=X/(V0*Cos(A)),
подстановкой получаем:
Y=X*Tan(A)-X/(V0*Cos(A)).
Дальность полета:
Xmax=V0^2/g*Sin(2*A).

Интерфейс программы.

Всего на форме 6 объектов:

  1. TextLabel1.text=»Угол А»
  2. TextLabel2.text=»Скорость V0″
  3. ComboBox1 — значения углов ограничим тремя значениями: 30, 45 и 60 градусов (свойство List).
  4. ComboBox2 — значение начальной скорости ограничим значениями в 50, 60 и 75 м/с.
  5. Объект рисования — DrawingArea1. Экпериментальными запусками снаряда, максимальную высоту и дальность определили в 300 на 600 точек экрана (метры).
  6. Кнопка Button1.text=»Огонь!»

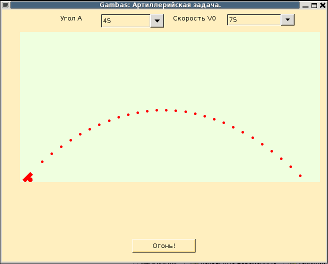
Результат:

Программа.

‘ Gambas class file
‘Глобальные переменные, видны во всех процедурах данной формы
PUBLIC CONST g AS Float = 9.8
‘константа, ускорение свободного падения
PUBLIC v0 AS Float
PUBLIC a AS Float

PUBLIC x AS Float
PUBLIC y AS Float
‘первичная инициализация свойст объектов
PUBLIC SUB _new()
  Combobox1.Index = 0 ‘нач. значение A
  Combobox2.Index = 0 ‘нач. знач. скорости — V0
  DrawingArea1.Height = 300 ‘высота объекта рисования
  DrawingArea1.Width = 600 ‘ширина
  ‘DrawingArea1.ForeColor = 16711937 ‘красный цвет снаряда
  DrawingArea1.Foreground = 16711680 ‘ цвет фона — светлозеленый
END

PUBLIC SUB Button1_Click()
DIM i AS Integer
‘знач. угла из списка
FOR i = 0 TO Combobox1.Count — 1
    IF Combobox1.Index = i THEN
        a = Combobox1.List[i]
    END IF
NEXT
‘знач. нач. скорости — V0
FOR i = 0 TO Combobox2.Count — 1
    IF Combobox2.Index = i THEN
        v0 = Combobox2.List[i]
    END IF
NEXT
‘переводим градусы в радианы
a = (Pi * a) / 180
x = 25
y = 0
pushkaTraektoria ‘вызываем процедуру (без параметров) построения — "PushkaTraektoria"
END

PRIVATE SUB pushkaTraektoria()

DIM pushka AS integer[] ‘создаем переменную: массив тип Integer
pushka = NEW integer[](8) ‘создаем новый объект, размерность массива — 8 элементов
pushka[0] = 5 ‘присваиваем элементам координаты многоугольника (пушка), значение X1
pushka[1] = 295 ‘Y1
pushka[2] = 20 ‘X2
pushka[3] = 280 ‘Y2
pushka[4] = 25 ‘X3
pushka[5] = 285 ‘Y3
pushka[6] = 10 ‘X4
pushka[7] = 300 ‘Y4

Draw.Begin(DrawingArea1) ‘Метод "Начать"
Draw.fillstyle = TRUE ‘закраска снарядов и контура пушки
Draw.fillcolor = 16711937 ‘красный цвет снарядов
Draw.Polygon(pushka) ‘Рисуем пушку
Draw.Circle(20, 295, 5) ‘рисуем колесо орудия
DO WHILE y >= 0 ‘Пока "снаряд" над землей, повторять
  x = x + ((v0 ^ 2 * Sin(2 * a)) / g) / 30
‘ делим на 30, по числу "снарядов" и прибавляем к предыдущему результату
  y = x * Tan(a) — (g * x ^ 2) / (2 * v0 ^ 2 * Cos(a) ^ 2)
  Draw.Circle(x, 300 — y, 3)
‘строим окружности описывающие траекторию движения снаряда
LOOP ‘конец цикла
Draw.End()
END SUB

Домашнее задание.
Запрограммируйте эффект взрыва — соприкосновение снаряда с поверхностью.
Используйте графический метод построения многоугольника Polygon.

Приложение: Архив программы

Подписаться на комментарии RSS 2.0. You can leave a response, or trackback from your own site.

Оставьте комментарий