Gambas. Еще один подход к артиллерийской задаче.
Методические материалы, Опыт работы с ПСПОАвтор: Владимир Черный
Публикуемая ниже разработка урока подготовлена учителем информатики МБОУ «Гимназия №85» г. Барнаула (Алтайский край) Чупиной Татьяной Ивановной, известной уже читателям блога по уроку «Метод Монте-Карло на уроке информатики». Далее идет текст автора.
Проект «Артиллерийская задача. Движение тела, брошенного под углом к горизонту» автора — Олега Чебан из из г. Киселевск Кемеровской области, безусловно интересный и позволяет избежать затруднений в графическом представлении описываемого процесса. Но не решает задачу сформулированную в учебнике Угриновича Н. Д. — 11 класс профильный уровень1. Нет выводов о попадании, невозможно оценить результат при тестовых параметрах задаваемых автором учебника. Предлагаю своё решение. Безусловно сославшись на вышеуказанного автора, как на первоисточник.
Мне как и многим учителям интереснее и полезнее видеть «листинг» программы, методика преподавания у каждого своя и во многом зависит от подготовки учителя и его учеников. В связи с этим не вижу смысла оформлять конспект урока, предлагаю план ключевых моментов урока.
1 этап (это один из первых уроков поэтому целесообразно повторить материал прошлого года относящийся к теме).
Повторение логических операций: конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание.
Редактор электронных таблиц, функции в Calc, логические функции.
2 этап — постановка задачи, этапы моделирования, вывод формул. Это достаточно подробно описано в учебнике.
3 этап — компьютерная модель в среде электронных таблиц.
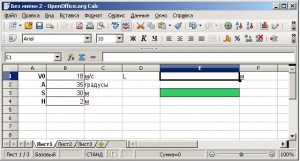
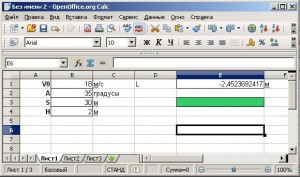
В параграфе представлено множество вспомогательных программ, расчетов и соответственно интерфейсов, которые между собой очень похожи. Дабы избежать путаницы все создаваемые компьютерные модели будем оформлять в едином стиле. На странице 21 учебника представлен интерфейс наиболее соответствующий целям проекта — возьмём за основу его.
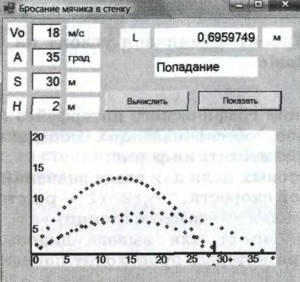
Данные в столбце В заполните, как в учебнике. В ячейку Е1 введите формулу 1.2 со страницы 16.
Сравните значение ячейки Е1 с результатом в учебнике — 0,6959749.
Для того чтобы найти причину несоответствия, я предлагаю ученикам следующее задание:
- сравните Pi/2 и 900 (равны)
- найдите sin(Pi/2) и sin(900) (равны единице)
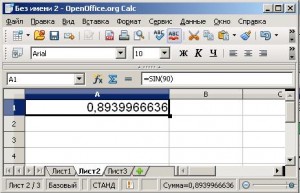
- найдите значение в среде электронных таблиц sin(900)
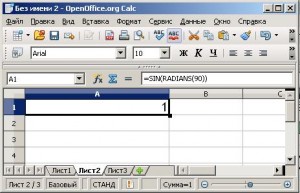
Выясняем, что радианная и градусная мера в среде электронных таблиц отличаются, и правильные расчеты производятся с радианной мерой угла. А в задаче мы используем градусную. Ищем функцию преобразующую градусы в радианы: =SIN(RADIANS(90))
Вносим изменения в формулу ячейки Е1:
=B3*TAN(RADIANS(B2))-(9,8*B3^2)/(2*B1^2*COS(RADIANS(B2))^2)
Задание:
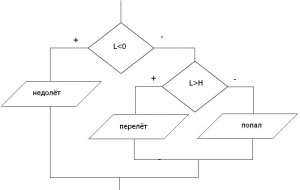
Составьте фрагмент блок-схемы условий.
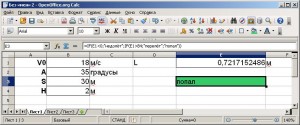
Самостоятельно введите формулу в зелёную ячейку, таким образом, что бы в зависимости от L, выводилось сообщение «попал», «недолёт», «перелёт». Условия попадания были рассмотрены раньше на странице 16.
Блок-схема.
Формула: =IF(E1<0;"недолёт";IF(E1>B4;»перелёт»;»попал»))
4 этап — компьютерная модель в среде Gambas.
Исходя из того что это один из первых уроков и будучи уверенной, что учащиеся не осилят графическую составляющую этой задачи (построение траектории движения в зависимости от параметров), я предложила воспользоваться проектом «Артиллерийская задача. Движение тела, брошенного под углом к горизонту» автора — Олега Чебан из из г. Киселевск Кемеровской области.
«Листинг» программы в электронном виде был доступен ученикам на сайте, поэтому реализация проекта не заняла много времени. Обсудив текст программы, повторив основные моменты учащиеся приступили к созданию собственного проекта со страницы 21.
Интерфейс программы:
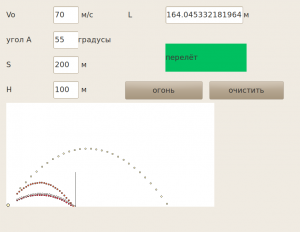
Примечания по программе:
- В программе заменили «пушку» — «точкой», так как при малых значениях S построения происходили позади «пушки». Изображение минимизировали.
- Организовали построение преграды-стены, что бы наглядно видеть результат.
-
Реализовано построение различных траекторий — разными цветами с помощью генератора случайных чисел:
Draw.FillColor = Color.RGB(Rnd(Date)*255, Rnd(Date)*255, Rnd(Date)*255). - При большом количестве испытаний траектории плохо просматриваются, поэтому создана кнопка «Очистить».
Программа:
' Gambas class file
PUBLIC CONST g AS Float = 9.8
PUBLIC v0 AS Float
PUBLIC a AS Float
PUBLIC s AS Float
PUBLIC h AS Float
PUBLIC l AS Float
PUBLIC x AS Float
PUBLIC y AS Float
PUBLIC SUB _new()
DrawingArea1.Height = 300
DrawingArea1.Width = 600
END
PUBLIC SUB Form_Open()
END
PUBLIC SUB Button1_Click()
v0 = Val(TextBox1.Text)
a = Val(TextBox2.Text)
s = Val(TextBox3.Text)
h = Val(TextBox4.Text)
a = (Pi * a) / 180
x = 25
y = 0
pushkaTraektoria
l = S * Tan(a) - (g * s ^ 2) / (2 * v0 ^ 2 * Cos(a) ^ 2)
TextBox5.Text = l
IF l < 0 THEN
Label11.text = "недолёт"
ELSE
IF l > h THEN
Label11.text = "перелёт"
ELSE
Label11.text = "попал"
END IF
END IF
END
PRIVATE SUB pushkaTraektoria()
Draw.Begin(DrawingArea1)
Draw.FillStyle = 1
Draw.FillColor = Color.RGB(Rnd(Date)*255, Rnd(Date)*255, Rnd(Date)*255)
Draw.Circle(5, 295, 5)
DO WHILE y >= 0
x = x + ((v0 ^ 2 * Sin(2 * a)) / g) / 30
y = x * Tan(a) - (g * x ^ 2) / (2 * v0 ^ 2 * Cos(a) ^ 2)
Draw.Circle(x, 300 - y, 3)
LOOP
Draw.Line(s, 300, s, 300 - h)
Draw.End()
END SUB
PUBLIC SUB Button2_Click()
DrawingArea1.Clear
END
Приложение: Проект Gambas
1Угринович Н. Д.
У27 Информатика и Икт. Профильный уровень: учебник для 11 класса. — 2 издание., испр. и доп. — М.:БИНОМ. Лаборатория знаний, 2009.-308 с.
ISBN 978-5-9963-0047-1



Октябрь 20, 2012, 1:09 пп
Замечания принимаются автором «первоисточника»
Задача, действительная интересна, на нее натолкнулся впервые в учебнике Гейна за 9-10 класс, только без графического решения. Однако, чтобы заинтересовать не слишком заинтересованных учащихся, пошел на хитрость и предложил графическую реализацию. Ошибки признаю!
С уважением, учитель информатики МБОУ «Гимназия №166″ г. Новоалтайска, Алтайского края, Чебан ОО